Перпендикулярность прямых в пространстве. Визуальный гид (2019). Перпендикулярные плоскости, условие перпендикулярности плоскостей Как определить что плоскости перпендикулярны

Данный урок поможет желающим получить представление о теме «Признак перпендикулярности двух плоскостей». В начале него мы повторим определение двугранного и линейного угла. Затем рассмотрим, какие плоскости называются перпендикулярными, и докажем признак перпендикулярности двух плоскостей.

Тема: Перпендикулярность прямых и плоскостей

Урок: Признак перпендикулярности двух плоскостей

Определение. Двугранным углом называется фигура, образованная двумя полуплоскостями, не принадлежащими одной плоскости, и их общей прямой а (а - ребро).

Рис. 1

Рассмотрим две полуплоскости α и β (рис. 1). Их общая граница - l. Указанная фигура называется двугранным углом. Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.

Двугранный угол измеряется своим линейным углом. На общем ребре l двугранного угла выберем произвольную точку. В полуплоскостях α и β из этой точки проведем перпендикуляры a и b к прямой l и получим линейный угол двугранного угла.

Прямые a и b образуют четыре угла, равных φ, 180° - φ, φ, 180° - φ. Напомним, углом между прямыми называется наименьший из этих углов.

Определение. Углом между плоскостями называется наименьший из двугранных углов, образованных этими плоскостями. φ - угол между плоскостями α и β, если

Определение. Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°.

Рис. 2

На ребре l выбрана произвольная точка М (рис. 2). Проведем две перпендикулярные прямые МА = а и МВ = b к ребру l в плоскости α и в плоскости β соответственно. Получили угол АМВ. Угол АМВ - это линейный угол двугранного угла. Если угол АМВ равен 90°, то плоскости α и β называются перпендикулярными.

Прямая b перпендикулярна прямой l по построению. Прямая b перпендикулярна прямой а, так как угол между плоскостями α и β равен 90°. Получаем, что прямая b перпендикулярна двум пересекающимся прямым а и l из плоскости α. Значит, прямая b перпендикулярна плоскости α.

Аналогично можно доказать, что прямая а перпендикулярна плоскости β. Прямая а перпендикулярна прямой l по построению. Прямая а перпендикулярна прямой b, так как угол между плоскостями α и β равен 90°. Получаем, что прямая а перпендикулярна двум пересекающимся прямым b и l из плоскости β. Значит, прямая а перпендикулярна плоскости β.

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Доказать:

Рис. 3

Доказательство:

Пусть плоскости α и β пересекаются по прямой АС (рис. 3). Чтобы доказать, что плоскости взаимно перпендикулярны, нужно построить линейный угол между ними и показать, что этот угол равен 90°.

Прямая АВ перпендикулярна по условию плоскости β, а значит, и прямой АС, лежащей в плоскости β.

Проведем прямую АD перпендикулярно прямой АС в плоскости β. Тогда ВАD -линейный угол двугранного угла.

Прямая АВ перпендикулярна плоскости β, а значит, и прямой АD, лежащей в плоскости β. Значит, линейный угол ВАD равен 90°. Значит, плоскости α и β перпендикулярны, что и требовалось доказать.

Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей (рис. 4).

Доказать:

Рис. 4

Доказательство:

Прямая l перпендикулярна плоскости γ, а плоскость α проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости α и γ перпендикулярны.

Прямая l перпендикулярна плоскости γ, а плоскость β проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости β и γ перпендикулярны.

Перпендикулярность в пространстве могут иметь:

1. Две прямые

3. Две плоскости

Давай по очереди рассмотрим эти три случая: все относящиеся к ним определения и формулировки теорем. А потом обсудим очень важную теорему о трёх перпендикулярах.

Перпендикулярность двух прямых.

Определение:

Ты можешь сказать: тоже мне, открыли Америку! Но вспомни, что в пространстве всё не совсем так, как на плоскости.

На плоскости перпендикулярными могут оказаться только такие прямые (пересекающиеся):

А вот перпендикулярность в пространстве двух прямых может быть даже в случае если они не пересекаются. Смотри:

прямая перпендикулярна прямой, хотя и не пересекается с нею. Как так? Вспоминаем определение угла между прямыми: чтобы найти угол между скрещивающимися прямыми и, нужно через произвольную точку на прямой a провести прямую. И тогда угол между и (по определению!) будет равен углу между и.

Вспомнили? Ну вот, а в нашем случае - если окажутся перпендикулярны прямые и, то нужно считать перпендикулярными прямые и.

Для полной ясности давай рассмотрим пример. Пусть есть куб. И тебя просят найти угол между прямыми и. Эти прямые не пересекаются - они скрещиваются. Чтобы найти угол между и, проведём.

Из-за того, что - параллелограмм (и даже прямоугольник!), получается, что. А из-за того, что - квадрат, выходит, что. Ну, и значит.

Перпендикулярность прямой и плоскости.

Определение:

Вот картинка:

прямая перпендикулярна плоскости, если она перпендикулярна всем-всем прямым в этой плоскости: и, и, и, и даже! И ещё миллиарду других прямых!

Да, но как же тогда вообще можно проверить перпендикулярность в прямой и плоскости? Так и жизни не хватит! Но на наше счастье математики избавили нас от кошмара бесконечности, придумав признак перпендикулярности прямой и плоскости .

Формулируем:

Оцени, как здорово:

если найдутся всего лишь две прямые (и) в плоскости, которым перпендикулярна прямая, то эта прямая сразу окажется перпендикулярна плоскости, то есть всем прямым в этой плоскости (в том числе и какой-то стоящей сбоку прямой). Это очень важная теорема, поэтому нарисуем её смысл ещё и в виде схемы.

И опять рассмотрим пример .

Пусть нам дан правильный тетраэдр.

Задача: доказать, что. Ты скажешь: это же две прямые! При чём же здесь перпендикулярность прямой и плоскости?!

А вот смотри:

давай отметим середину ребра и проведём и. Это медианы в и. Треугольники - правильные и.

Вот оно, чудо: получается, что, так как и. И далее, всем прямым в плоскости, а значит, и. Доказали. И самым главным моментом оказалось именно применение признака перпендикулярности прямой и плоскости.

Когда плоскости перпендикулярны

Определение:

То есть (подробнее смотри в теме «двугранный угол») две плоскости (и) перпендикулярны, если окажется, что угол между двумя перпендикулярами (и) к линии пересечения этих плоскостей равен. И есть теорема, которая связывает понятие перпендикулярных плоскостей с понятием перпендикулярность в пространстве прямой и плоскости.

Теорема эта называется

Критерий перпендикулярности плоскостей.

Давай сформулируем:

Как всегда, расшифровка слов «тогда и только тогда» выглядит так:

Если, то проходит через перпендикуляр к.

Если проходит через перпендикуляр к, то.

(естественно, здесь и - плоскости).

Эта теорема - одна из самых важных в стереометрии, но, к сожалению, и одна из самых непростых в применении.

Так что нужно быть очень внимательным!

Итак, формулировка:

И снова расшифровка слов «тогда и только тогда». Теорема утверждает сразу две вещи (смотри на картинку):

давай попробуем применить эту теорему для решения задачи.

Задача : дана правильная шестиугольная пирамида. Найти угол между прямыми и.

Решение:

Из-за того, что в правильной пирамиде вершина при проекции попадает в центр основания, оказывается, что прямая - проекция прямой.

Но мы знаем, что в правильном шестиугольнике. Применяем теорему о трёх перпендикулярах:

И пишем ответ: .

ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ. КОРОТКО О ГЛАВНОМ

Перпендикулярность двух прямых.

Две прямые в пространстве перпендикулярны, если угол между ними.

Перпендикулярность прямой и плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна всем прямым в этой плоскости.

Перпендикулярность плоскостей.

Плоскости перпендикулярны, если двугранный угол между ними равен.

Критерий перпендикулярности плоскостей.

Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через перпендикуляр к другой плоскости.

Теорема о трех перпендикулярах:

Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.

Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.

Проблема в том, что этого может не хватить…

Для чего?

Для успешной сдачи ЕГЭ, для поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…

Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.

Но и это - не главное.

Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю...

Но, думай сам...

Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?

НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.

На экзамене у тебя не будут спрашивать теорию.

Тебе нужно будет решать задачи на время .

И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.

Это как в спорте - нужно много раз повторить, чтобы выиграть наверняка.

Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!

Можно воспользоваться нашими задачами (не обязательно) и мы их, конечно, рекомендуем.

Для того, чтобы набить руку с помощью наших задач нужно помочь продлить жизнь учебнику YouClever, который ты сейчас читаешь.

Как? Есть два варианта:

Открой доступ ко всем скрытым задачам в этой статье -
Открой доступ ко всем скрытым задачам во всех 99-ти статьях учебника - Купить учебник - 899 руб

Да, у нас в учебнике 99 таких статей и доступ для всех задач и всех скрытых текстов в них можно открыть сразу.

Доступ ко всем скрытым задачам предоставляется на ВСЕ время существования сайта.

И в заключение...

Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.

“Понял” и “Умею решать” - это совершенно разные навыки. Тебе нужны оба.

Найди задачи и решай!

Понятие перпендикулярных плоскостей

При пересечении двух плоскостей у нас получается $4$ двугранных угла. Два угла равны $\varphi $, а два другие равны ${180}^0-\varphi $.

Определение 1

Углом между плоскостями называется минимальный из двугранных углов, образованных этими плоскостями.

Определение 2

Две пересекающиеся плоскости называются перпендикулярными, если угол между этими плоскостями равен $90^\circ$ (рис. 1).

Рисунок 1. Перпендикулярные плоскости

Признак перпендикулярности двух плоскостей

Теорема 1

Если прямая плоскости перпендикулярна другой плоскости, то эти плоскости перпендикулярны друг другу.

Доказательство.

Пусть нам даны плоскости $\alpha $ и $\beta $, которые пересекаются по прямой $AC$. Пусть прямая $AB$, лежащая в плоскости $\alpha $ перпендикулярна плоскости $\beta $ (рис. 2).

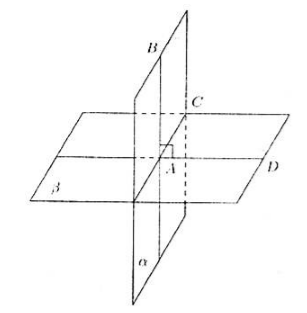
Рисунок 2.

Так как прямая $AB$ перпендикулярна плоскости $\beta $, то она перпендикулярна и прямой $AC$. Проведем дополнительно прямую $AD$ в плоскости $\beta $, перпендикулярно прямой $AC$.

Получаем, что угол $BAD$ - линейный угол двугранного угла, равный $90^\circ$. То есть, по определению 1, угол между плоскостями равен $90^\circ$, значит, данные плоскости перпендикулярны.

Теорема доказана.

Из этой теоремы следует следующая теорема.

Теорема 2

Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.

Доказательство.

Пусть нам даны две плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Плоскость $\gamma $ перпендикулярна прямой $c$ (рис. 3)

Рисунок 3.

Так как прямая $c$ принадлежит плоскости $\alpha $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\alpha $ и $\gamma $ перпендикулярны.

Так как прямая $c$ принадлежит плоскости $\beta $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\beta $ и $\gamma $ перпендикулярны.

Теорема доказана.

Для каждой из этих теорем справедливы и обратные утверждения.

Примеры задач

Пример 1

Пусть нам дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Найти все пары перпендикулярных плоскостей (рис. 5).

Рисунок 4.

Решение.

По определению прямоугольного параллелепипеда и перпендикулярных плоскостей видим следующие восемь пар перпендикулярных между собой плоскостей: $(ABB_1)$ и $(ADD_1)$, $(ABB_1)$ и $(A_1B_1C_1)$, $(ABB_1)$ и $(BCC_1)$, $(ABB_1)$ и $(ABC)$, $(DCC_1)$ и $(ADD_1)$, $(DCC_1)$ и $(A_1B_1C_1)$, $(DCC_1)$ и $(BCC_1)$, $(DCC_1)$ и $(ABC)$.

Пример 2

Пусть нам даны две взаимно перпендикулярные плоскости. Из точки одной плоскости проведен перпендикуляр к другой плоскости. Доказать, что эта прямая лежит в данной плоскости.

Доказательство.

Пусть нам даны перпендикулярные плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Из точки $A$ плоскости $\beta $ проведен перпендикуляр $AC$ к плоскости $\alpha $. Предположим, что $AC$ не лежит в плоскости $\beta $ (рис. 6).

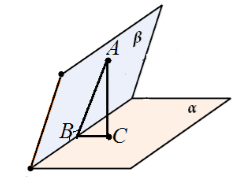
Рисунок 5.

Рассмотрим треугольник $ABC$. Он является прямоугольным с прямым углом $ACB$. Следовательно, $\angle ABC\ne {90}^0$.

Но, с другой стороны, $\angle ABC$ является линейным углом двугранного угла, образованного этими плоскостями. То есть двугранный угол, образованный этими плоскостями не равняется 90 градусам. Получаем, что угол между плоскостями не равен $90^\circ$. Противоречие. Следовательно, $AC$ лежит в плоскости $\beta $.

Тема: Перпендикулярность прямых и плоскостей

Урок: Признак перпендикулярности двух плоскостей

Рис. 1

Рис. 2

Доказать:

Рис. 3

Доказательство:

Прямая АВ перпендикулярна по условию плоскости β, а значит, и прямой АС, лежащей в плоскости β.

Проведем прямую АD перпендикулярно прямой АС в плоскости β. Тогда ВАD -линейный угол двугранного угла.

Доказать:

Рис. 4

Доказательство: