Perpendularité des lignes dans l'espace. Guide visuel (2019). Plans perpendiculaires, la condition de perpendiculaire des plans Comment déterminer que les plans sont perpendiculaires

Cette leçon aidera ceux qui souhaitent comprendre le sujet « Le signe de la perpendiculaire de deux plans ». Au début, nous répéterons la définition des angles dièdres et linéaires. Ensuite, nous considérerons quels plans sont appelés perpendiculaires et prouverons le signe de perpendiculaire de deux plans.

Sujet : Perpendiculaire des lignes et des plans

Leçon : Signe de perpendiculaire de deux plans

Définition. Un angle dièdre est une figure formée de deux demi-plans n'appartenant pas au même plan et de leur droite commune a (a est une arête).

Riz. 1

Considérons deux demi-plans α et β (Fig. 1). Leur frontière commune est l. Cette figure est appelée angle dièdre. Deux plans sécants forment quatre angles dièdres avec une arête commune.

Un angle dièdre est mesuré par son angle linéaire. On choisit un point arbitraire sur l'arête commune l de l'angle dièdre. Dans les demi-plans α et β, à partir de ce point on trace les perpendiculaires a et b à la droite l et on obtient l'angle linéaire de l'angle dièdre.

Les droites a et b forment quatre angles égaux à φ, 180° - φ, φ, 180° - φ. Rappelons que l'angle entre les droites est le plus petit de ces angles.

Définition. L'angle entre plans est le plus petit des angles dièdres formés par ces plans. φ est l'angle entre les plans α et β, si

Définition. Deux plans qui se croisent sont dits perpendiculaires ( mutuellement perpendiculaires ) si l'angle entre eux est de 90°.

Riz. 2

Un point arbitraire M est sélectionné sur le bord l (Fig. 2). Traçons deux droites perpendiculaires MA = a et MB = b au bord l dans le plan α et dans le plan β, respectivement. Nous avons l'angle AMB. L'angle AMB est l'angle linéaire d'un angle dièdre. Si l'angle AMB est de 90°, alors les plans α et β sont dits perpendiculaires.

La ligne b est perpendiculaire à la ligne l par construction. La droite b est perpendiculaire à la droite a, puisque l’angle entre les plans α et β est de 90°. Nous constatons que la droite b est perpendiculaire à deux droites sécantes a et l à partir du plan α. Cela signifie que la droite b est perpendiculaire au plan α.

De même, on peut prouver que la droite a est perpendiculaire au plan β. La ligne a est perpendiculaire à la ligne l par construction. La droite a est perpendiculaire à la droite b, puisque l’angle entre les plans α et β est de 90°. Nous constatons que la droite a est perpendiculaire à deux droites sécantes b et l à partir du plan β. Cela signifie que la droite a est perpendiculaire au plan β.

Si l’un des deux plans passe par une ligne perpendiculaire à l’autre plan, alors ces plans sont perpendiculaires.

Prouver:

Riz. 3

Preuve:

Laissez les plans α et β se couper le long de la droite AC (Fig. 3). Pour prouver que les plans sont perpendiculaires entre eux, il faut construire un angle linéaire entre eux et montrer que cet angle est de 90°.

La droite AB est perpendiculaire au plan β, et donc à la droite AC située dans le plan β.

Traçons une droite AD perpendiculaire à une droite AC dans le plan β. Alors BAD est l’angle linéaire de l’angle dièdre.

La droite AB est perpendiculaire au plan β, et donc à la droite AD située dans le plan β. Cela signifie que l'angle linéaire BAD est de 90°. Cela signifie que les plans α et β sont perpendiculaires, ce qu’il fallait prouver.

Le plan perpendiculaire à la ligne le long de laquelle deux plans donnés se coupent est perpendiculaire à chacun de ces plans (Fig. 4).

Prouver:

Riz. 4

Preuve:

La droite l est perpendiculaire au plan γ et le plan α passe par la droite l. Cela signifie que, sur la base de la perpendiculaire des plans, les plans α et γ sont perpendiculaires.

La droite l est perpendiculaire au plan γ et le plan β passe par la droite l. Cela signifie que selon la perpendiculaire des plans, les plans β et γ sont perpendiculaires.

La perpendiculaire dans l’espace peut avoir :

1. Deux lignes droites

3. Deux avions

Regardons ces trois cas tour à tour : toutes les définitions et énoncés des théorèmes qui s'y rapportent. Et puis nous discuterons du théorème très important sur les trois perpendiculaires.

Perpendiculaire de deux lignes.

Définition:

On peut dire : ils ont découvert l’Amérique aussi pour moi ! Mais rappelez-vous que dans l’espace, tout n’est pas exactement comme dans un avion.

Sur un plan, seules les droites suivantes (se coupant) peuvent être perpendiculaires :

Mais deux droites peuvent être perpendiculaires dans l’espace même si elles ne se coupent pas. Regarder:

une ligne droite est perpendiculaire à une ligne droite, même si elle ne la coupe pas. Comment ça? Rappelons la définition de l'angle entre droites : pour trouver l'angle entre droites qui se croisent et, il faut tracer une droite passant par un point arbitraire de la droite a. Et puis l’angle entre et (par définition !) sera égal à l’angle entre et.

Vous souvenez-vous? Eh bien, dans notre cas, si les lignes droites et s'avèrent perpendiculaires, alors nous devons considérer les lignes droites et perpendiculaires.

Pour plus de clarté, regardons exemple. Qu'il y ait un cube. Et il vous est demandé de trouver l'angle entre les lignes et. Ces lignes ne se coupent pas – elles se coupent. Pour trouver l'angle entre et, dessinons.

Du fait qu'il s'agit d'un parallélogramme (et même d'un rectangle !), il s'avère que c'est le cas. Et comme il s’agit d’un carré, il s’avère que c’est le cas. Eh bien, ça veut dire.

Perpendiculaire d'une droite et d'un plan.

Définition:

Voici une photo :

une droite est perpendiculaire à un plan si elle est perpendiculaire à toutes, toutes les droites de ce plan : et, et, et, et pair ! Et un milliard d’autres lignes directes !

Oui, mais comment alors vérifier de manière générale la perpendiculaire dans une ligne droite et dans un plan ? Alors la vie ne suffit pas ! Mais heureusement pour nous, les mathématiciens nous ont sauvés du cauchemar de l'infini en inventant signe de perpendiculaire d'une droite et d'un plan.

Formulons :

Évaluez à quel point c'est génial :

s'il n'y a que deux droites (et) dans le plan auquel la droite est perpendiculaire, alors cette droite se révélera immédiatement perpendiculaire au plan, c'est-à-dire à toutes les droites de ce plan (y compris certaines droites ligne debout sur le côté). Il s’agit d’un théorème très important, nous allons donc également en tracer la signification sous forme de diagramme.

Et regardons encore exemple.

Donnons-nous un tétraèdre régulier.

Tâche : prouver cela. Vous direz : ce sont deux lignes droites ! Qu’est-ce que la perpendiculaire d’une droite et d’un plan a à voir là-dedans ?!

Mais regarde :

marquons le milieu du bord et dessinons et. Ce sont les médianes dans et. Les triangles sont réguliers et...

Voilà, un miracle : il s'avère que, depuis et. Et plus loin, à toutes les lignes droites du plan, ce qui signifie et. Ils l'ont prouvé. Et le point le plus important était justement l’utilisation du signe de perpendiculaire d’une droite et d’un plan.

Quand les plans sont perpendiculaires

Définition:

C'est-à-dire (pour plus de détails, voir le sujet « angle dièdre ») deux plans (et) sont perpendiculaires s'il s'avère que l'angle entre deux perpendiculaires (et) à la ligne d'intersection de ces plans est égal. Et il existe un théorème qui relie le concept de plans perpendiculaires au concept de perpendiculaire dans l'espace d'une ligne et d'un plan.

Ce théorème s'appelle

Critère de perpendiculaire des plans.

Formulons :

Comme toujours, le décodage des mots « alors et seulement alors » ressemble à ceci :

Si, alors passe par la perpendiculaire à.

S'il passe par la perpendiculaire à, alors.

(naturellement, nous sommes ici des avions).

Ce théorème est l’un des plus importants en stéréométrie, mais malheureusement aussi l’un des plus difficiles à appliquer.

Il faut donc être très prudent !

Ainsi, la formulation :

Et encore une fois, déchiffrer les mots « alors et alors seulement ». Le théorème énonce deux choses à la fois (regardez l'image) :

essayons d'appliquer ce théorème pour résoudre le problème.

Tâche: une pyramide hexagonale régulière est donnée. Trouvez l'angle entre les lignes et.

Solution:

Du fait que dans une pyramide régulière, le sommet, lorsqu'il est projeté, tombe au centre de la base, il s'avère que la ligne droite est une projection de la ligne droite.

Mais on sait que c'est dans un hexagone régulier. On applique le théorème des trois perpendiculaires :

Et nous écrivons la réponse : .

PERPENDICULARITÉ DES LIGNES DROITES DANS L'ESPACE. EN BREF SUR LES CHOSES PRINCIPALES

Perpendiculaire de deux lignes.

Deux droites dans l’espace sont perpendiculaires s’il existe un angle entre elles.

Perpendiculaire d'une droite et d'un plan.

Une droite est perpendiculaire à un plan si elle est perpendiculaire à toutes les droites de ce plan.

Perpendiculaire des plans.

Les plans sont perpendiculaires si l'angle dièdre entre eux est égal.

Critère de perpendiculaire des plans.

Deux plans sont perpendiculaires si et seulement si l’un d’eux passe par la perpendiculaire à l’autre plan.

Théorème des trois perpendiculaires :

Eh bien, le sujet est terminé. Si vous lisez ces lignes, c’est que vous êtes très cool.

Parce que seulement 5 % des gens sont capables de maîtriser quelque chose par eux-mêmes. Et si vous lisez jusqu'au bout, alors vous êtes dans ces 5% !

Maintenant, le plus important.

Vous avez compris la théorie sur ce sujet. Et je le répète, ça... c'est juste super ! Vous êtes déjà meilleur que la grande majorité de vos pairs.

Le problème est que cela ne suffit peut-être pas...

Pour quoi?

Pour avoir réussi l'examen d'État unifié, pour entrer à l'université avec un budget limité et, SURTOUT, pour la vie.

Je ne vais vous convaincre de rien, je dirai juste une chose...

Les personnes qui ont reçu une bonne éducation gagnent beaucoup plus que celles qui ne l’ont pas reçue. Ce sont des statistiques.

Mais ce n’est pas l’essentiel.

L'essentiel est qu'ils soient PLUS HEUREUX (il existe de telles études). Peut-être parce que de nombreuses autres opportunités s'ouvrent devant eux et que la vie devient plus lumineuse ? Je ne sais pas...

Mais pensez par vous-même...

Que faut-il pour être sûr d'être meilleur que les autres à l'examen d'État unifié et finalement être... plus heureux ?

GAGNEZ VOTRE MAIN EN RÉSOUDANT DES PROBLÈMES SUR CE SUJET.

Aucune théorie ne vous sera demandée lors de l'examen.

Vous aurez besoin résoudre des problèmes contre le temps.

Et si vous ne les avez pas résolus (BEAUCOUP !), vous ferez certainement une erreur stupide quelque part ou vous n’aurez tout simplement pas le temps.

C'est comme dans le sport : il faut répéter plusieurs fois pour gagner avec certitude.

Retrouvez la collection où vous voulez, nécessairement avec des solutions, une analyse détaillée et décidez, décidez, décidez !

Vous pouvez utiliser nos tâches (facultatif) et nous les recommandons bien sûr.

Afin de mieux utiliser nos tâches, vous devez contribuer à prolonger la durée de vie du manuel YouClever que vous lisez actuellement.

Comment? Il existe deux options :

Débloquez toutes les tâches cachées dans cet article -
Débloquez l'accès à toutes les tâches cachées dans les 99 articles du manuel - Acheter un manuel - 899 RUR

Oui, nous avons 99 articles de ce type dans notre manuel et l'accès à toutes les tâches et à tous les textes cachés qu'elles contiennent peut être ouvert immédiatement.

L'accès à toutes les tâches cachées est assuré pendant TOUTE la vie du site.

Et en conclusion...

Si vous n'aimez pas nos tâches, trouvez-en d'autres. Ne vous arrêtez pas à la théorie.

« Compris » et « Je peux résoudre » sont des compétences complètement différentes. Vous avez besoin des deux.

Trouvez les problèmes et résolvez-les !

Le concept de plans perpendiculaires

Lorsque deux plans se coupent, nous obtenons des angles dièdres de 4$. Deux angles sont égaux à $\varphi $ et les deux autres sont égaux à $(180)^0-\varphi $.

Définition 1

L'angle entre plans est le minimum des angles dièdres formés par ces plans.

Définition 2

Deux plans sécants sont dits perpendiculaires si l'angle entre ces plans est $90^\circ$ (Fig. 1).

Figure 1. Plans perpendiculaires

Signe de perpendiculaire de deux plans

Théorème 1

Si une droite d’un plan est perpendiculaire à un autre plan, alors ces plans sont perpendiculaires entre eux.

Preuve.

Donnons-nous les plans $\alpha $ et $\beta $, qui se coupent le long de la droite $AC$. Soit la droite $AB$ située dans le plan $\alpha $ soit perpendiculaire au plan $\beta $ (Fig. 2).

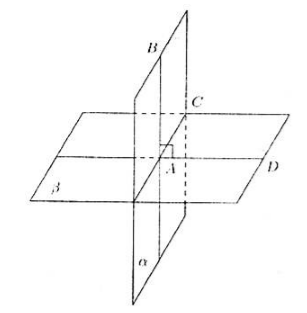
Graphique 2.

Puisque la droite $AB$ est perpendiculaire au plan $\beta$, elle est également perpendiculaire à la droite $AC$. Traçons en outre une droite $AD$ dans le plan $\beta$, perpendiculaire à la droite $AC$.

On constate que l'angle $BAD$ est l'angle linéaire de l'angle dièdre, égal à $90^\circ$. Autrement dit, par définition 1, l'angle entre les plans est $90^\circ$, ce qui signifie que ces plans sont perpendiculaires.

Le théorème a été prouvé.

Le théorème suivant découle de ce théorème.

Théorème 2

Si un plan est perpendiculaire à la ligne le long de laquelle deux autres plans se coupent, alors il est également perpendiculaire à ces plans.

Preuve.

Soit deux plans $\alpha $ et $\beta $ se coupant le long de la droite $c$. Le plan $\gamma $ est perpendiculaire à la droite $c$ (Fig. 3)

Graphique 3.

Puisque la droite $c$ appartient au plan $\alpha $ et que le plan $\gamma $ est perpendiculaire à la droite $c$, alors, d'après le théorème 1, les plans $\alpha $ et $\gamma $ sont perpendiculaires.

Puisque la droite $c$ appartient au plan $\beta $ et que le plan $\gamma $ est perpendiculaire à la droite $c$, alors, d'après le théorème 1, les plans $\beta $ et $\gamma $ sont perpendiculaires.

Le théorème a été prouvé.

Pour chacun de ces théorèmes, les affirmations inverses sont également vraies.

Exemples de problèmes

Exemple 1

Donnons-nous un parallélépipède rectangle $ABCDA_1B_1C_1D_1$. Trouvez toutes les paires de plans perpendiculaires (Fig. 5).

Graphique 4.

Solution.

Par la définition d'un parallélépipède rectangle et de plans perpendiculaires, on voit les huit paires de plans suivantes perpendiculaires entre elles : $(ABB_1)$ et $(ADD_1)$, $(ABB_1)$ et $(A_1B_1C_1)$, $( ABB_1)$ et $(BCC_1) $, $(ABB_1)$ et $(ABC)$, $(DCC_1)$ et $(ADD_1)$, $(DCC_1)$ et $(A_1B_1C_1)$, $(DCC_1) $ et $(BCC_1)$, $(DCC_1)$ et $(ABC)$.

Exemple 2

Soit deux plans perpendiculaires entre eux. À partir d’un point d’un plan, une perpendiculaire est tracée à un autre plan. Montrer que cette droite se trouve dans le plan donné.

Preuve.

Donnons-nous des plans perpendiculaires $\alpha $ et $\beta $ se coupant le long de la droite $c$. Du point $A$ du plan $\beta $ une perpendiculaire $AC$ est tracée au plan $\alpha $. Supposons que $AC$ ne se trouve pas dans le plan $\beta$ (Fig. 6).

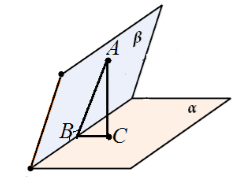
Graphique 5.

Considérons le triangle $ABC$. Il est rectangulaire à angle droit $ACB$. Par conséquent, $\angle ABC\ne (90)^0$.

Mais d'un autre côté, $\angle ABC$ est l'angle linéaire de l'angle dièdre formé par ces plans. C'est-à-dire que l'angle dièdre formé par ces plans n'est pas égal à 90 degrés. On constate que l'angle entre les plans n'est pas égal à $90^\circ$. Contradiction. Par conséquent, $AC$ se trouve dans le plan $\beta$.

Sujet : Perpendiculaire des lignes et des plans

Leçon : Signe de perpendiculaire de deux plans

Définition. Un angle dièdre est une figure formée de deux demi-plans n'appartenant pas au même plan et de leur droite commune a (a est une arête).

Riz. 1

Considérons deux demi-plans α et β (Fig. 1). Leur frontière commune est l. Cette figure est appelée angle dièdre. Deux plans sécants forment quatre angles dièdres avec une arête commune.

Les droites a et b forment quatre angles égaux à φ, 180° - φ, φ, 180° - φ. Rappelons que l'angle entre les droites est le plus petit de ces angles.

Définition. L'angle entre plans est le plus petit des angles dièdres formés par ces plans. φ est l'angle entre les plans α et β, si

Définition. Deux plans qui se croisent sont dits perpendiculaires ( mutuellement perpendiculaires ) si l'angle entre eux est de 90°.

Riz. 2

Si l’un des deux plans passe par une ligne perpendiculaire à l’autre plan, alors ces plans sont perpendiculaires.

Prouver:

Riz. 3

Preuve:

La droite AB est perpendiculaire au plan β, et donc à la droite AC située dans le plan β.

Traçons une droite AD perpendiculaire à une droite AC dans le plan β. Alors BAD est l’angle linéaire de l’angle dièdre.

Le plan perpendiculaire à la ligne le long de laquelle deux plans donnés se coupent est perpendiculaire à chacun de ces plans (Fig. 4).

Prouver:

Riz. 4

Preuve:

La droite l est perpendiculaire au plan γ et le plan α passe par la droite l. Cela signifie que, sur la base de la perpendiculaire des plans, les plans α et γ sont perpendiculaires.

La droite l est perpendiculaire au plan γ et le plan β passe par la droite l. Cela signifie que selon la perpendiculaire des plans, les plans β et γ sont perpendiculaires.