Kolmost čar v prostoru. Vizuální průvodce (2019). Kolmé roviny, podmínka kolmosti rovin Jak určit, že roviny jsou kolmé

Tato lekce pomůže těm, kteří chtějí porozumět tématu „Znak kolmosti dvou rovin“. Na jeho začátku si zopakujeme definici dihedrálních a lineárních úhlů. Potom budeme uvažovat, které roviny se nazývají kolmé, a dokážeme znaménko kolmosti dvou rovin.

Téma: Kolmost přímek a rovin

Lekce: Znak kolmosti dvou rovin

Definice. Dihedrální úhel je obrazec tvořený dvěma polorovinami, které nepatří do stejné roviny, a jejich společnou přímkou ​​a (a je hrana).

Rýže. 1

Uvažujme dvě poloroviny α a β (obr. 1). Jejich společná hranice je l. Tento údaj se nazývá dihedrální úhel. Dvě protínající se roviny svírají čtyři dihedrální úhly se společnou hranou.

Dihedrální úhel se měří jeho lineárním úhlem. Zvolíme libovolný bod na společné hraně l úhlu dihedrálního úhlu. V polorovinách α a β vedeme z tohoto bodu kolmice a a b k přímce l a získáme lineární úhel úhlu vzepětí.

Přímky a a b svírají čtyři úhly rovné φ, 180° - φ, φ, 180° - φ. Připomeňme, že úhel mezi přímkami je nejmenší z těchto úhlů.

Definice. Úhel mezi rovinami je nejmenší z dihedrálních úhlů tvořených těmito rovinami. φ je úhel mezi rovinami α a β, jestliže

Definice. Dvě protínající se roviny se nazývají kolmé (vzájemně kolmé), pokud je mezi nimi úhel 90°.

Rýže. 2

Na hraně l je vybrán libovolný bod M (obr. 2). Nakreslete dvě kolmé přímky MA = a a MB = b k hraně l v rovině α a v rovině β. Máme úhel AMB. Úhel AMB je lineární úhel dihedrálního úhlu. Je-li úhel AMB 90°, pak se roviny α a β nazývají kolmé.

Čára b je konstrukčně kolmá na čáru l. Přímka b je kolmá k přímce a, protože úhel mezi rovinami α a β je 90°. Zjistíme, že přímka b je kolmá ke dvěma protínajícím se přímkám a a l z roviny α. To znamená, že přímka b je kolmá k rovině α.

Podobně můžeme dokázat, že přímka a je kolmá k rovině β. Přímka a je konstrukčně kolmá na přímku l. Přímka a je kolmá k přímce b, protože úhel mezi rovinami α a β je 90°. Zjistíme, že přímka a je kolmá na dvě protínající se přímky b a l z roviny β. To znamená, že přímka a je kolmá k rovině β.

Pokud jedna ze dvou rovin prochází přímkou ​​kolmou k druhé rovině, pak jsou takové roviny kolmé.

Dokázat:

Rýže. 3

Důkaz:

Nechť se roviny α a β protínají podél přímky AC (obr. 3). Abyste dokázali, že roviny jsou vzájemně kolmé, musíte mezi nimi sestrojit lineární úhel a ukázat, že tento úhel je 90°.

Přímka AB je kolmá k rovině β, a tedy k přímce AC ležící v rovině β.

Narýsujme přímku AD kolmou k přímce AC v rovině β. Potom BAD je lineární úhel dihedrálního úhlu.

Přímka AB je kolmá k rovině β, a tedy k přímce AD ​​ležící v rovině β. To znamená, že lineární úhel BAD je 90°. To znamená, že roviny α a β jsou kolmé, což bylo potřeba dokázat.

Rovina kolmá k přímce, podél které se protínají dvě dané roviny, je kolmá na každou z těchto rovin (obr. 4).

Dokázat:

Rýže. 4

Důkaz:

Přímka l je kolmá k rovině γ a rovina α prochází přímkou ​​l. To znamená, že na základě kolmosti rovin jsou roviny α a γ kolmé.

Přímka l je kolmá k rovině γ a rovina β prochází přímkou ​​l. To znamená, že podle kolmosti rovin jsou roviny β a γ kolmé.

Kolmost v prostoru může mít:

1. Dvě přímky

3. Dvě roviny

Podívejme se postupně na tyto tři případy: všechny definice a výroky vět, které se k nim vztahují. A pak probereme velmi důležitou větu o třech kolmicích.

Kolmost dvou čar.

Definice:

Dá se říct: i pro mě objevili Ameriku! Pamatujte ale, že ve vesmíru není všechno úplně stejné jako v letadle.

Na rovině mohou být kolmé pouze následující čáry (protínající se):

Ale dvě přímky mohou být v prostoru kolmé, i když se neprotínají. Podívejte:

přímka je kolmá k přímce, ačkoli se s ní neprotíná. jak to? Připomeňme si definici úhlu mezi přímkami: abyste našli úhel mezi protínajícími se čarami a, musíte nakreslit přímku přes libovolný bod na přímce a. A pak úhel mezi a (podle definice!) bude roven úhlu mezi a.

pamatuješ? No, v našem případě, pokud se přímky a přímky ukáží jako kolmé, pak musíme považovat přímky a být kolmé.

Pro úplnou přehlednost se podívejme na příklad. Ať je tam kostka. A budete požádáni, abyste našli úhel mezi čarami a. Tyto linie se neprotínají – protínají se. Chcete-li najít úhel mezi a, nakreslete.

Vzhledem k tomu, že se jedná o rovnoběžník (a dokonce i obdélník!), ukazuje se, že. A vzhledem k tomu, že je to čtverec, tak to dopadá. No, to znamená.

Kolmost přímky a roviny.

Definice:

Tady je obrázek:

přímka je kolmá k rovině, pokud je kolmá ke všem, všem přímkám v této rovině: a, a, a, a dokonce! A miliarda dalších přímých!

Ano, ale jak potom můžete obecně zkontrolovat kolmost v přímce a v rovině? Takže život nestačí! Ale naštěstí nás matematici zachránili před noční můrou nekonečna vynálezem znak kolmosti přímky a roviny.

Pojďme formulovat:

Ohodnoťte, jak je to skvělé:

pokud jsou v rovině, ke které je přímka kolmá, pouze dvě přímky (a), pak se tato přímka okamžitě ukáže jako kolmá k rovině, tedy ke všem přímkám v této rovině (včetně některých přímých čára stojící na straně). Jedná se o velmi důležitou větu, proto její význam nakreslíme také ve formě diagramu.

A podívejme se znovu příklad.

Dostaneme pravidelný čtyřstěn.

Úkol: dokaž to. Řeknete si: to jsou dvě rovné čáry! Co s tím má společného kolmost přímky a roviny?!

Ale podívej:

označíme střed okraje a nakreslíme a. Toto jsou mediány v a. Trojúhelníky jsou pravidelné a...

Tady to je, zázrak: ukázalo se, že od a. A dále na všechny přímky v rovině, což znamená a. Dokázali to. A tím nejdůležitějším bodem bylo právě použití znaku kolmosti přímky a roviny.

Když jsou roviny kolmé

Definice:

To znamená (pro více podrobností viz téma „úhel vzepětí“) dvě roviny (a) jsou kolmé, pokud se ukáže, že úhel mezi dvěma kolmicemi (a) k přímce průsečíku těchto rovin je stejný. A existuje věta, která spojuje pojem kolmých rovin s pojmem kolmost v prostoru přímky a roviny.

Tato věta se nazývá

Kritérium pro kolmost rovin.

Pojďme formulovat:

Jako vždy vypadá dekódování slov „pak a teprve potom“ takto:

• Pokud, pak prochází kolmicí k.

• Pokud prochází kolmicí k, pak.

(přirozeně, tady jsme letadla).

Tato věta je jednou z nejdůležitějších ve stereometrii, ale bohužel také jednou z nejobtížněji aplikovatelných.

Takže musíte být velmi opatrní!

Takže formulace:

A znovu dešifrování slov „pak a teprve potom“. Věta říká dvě věci najednou (podívejte se na obrázek):

zkusme použít tuto větu k vyřešení problému.

Úkol: je dán pravidelný šestiboký jehlan. Najděte úhel mezi čarami a.

Řešení:

Vzhledem k tomu, že v pravidelném jehlanu vrchol při promítání spadá do středu základny, ukazuje se, že přímka je průmětem přímky.

Ale víme, že je v pravidelném šestiúhelníku. Aplikujeme větu o třech kolmicích:

A napíšeme odpověď: .

KOLMOČNOST PŘÍMEK V PROSTORU. KRÁTCE O HLAVNÍCH VĚCÍCH

Kolmost dvou čar.

Dvě čáry v prostoru jsou kolmé, pokud je mezi nimi úhel.

Kolmost přímky a roviny.

Přímka je kolmá k rovině, pokud je kolmá ke všem přímkám v této rovině.

Kolmost rovin.

Roviny jsou kolmé, pokud je úhel mezi nimi stejný.

Kritérium pro kolmost rovin.

Dvě roviny jsou kolmé právě tehdy, když jedna z nich prochází kolmicí k druhé rovině.

Věta o třech kolmých:

No, téma skončilo. Pokud čtete tyto řádky, znamená to, že jste velmi cool.

Protože jen 5 % lidí je schopno něco zvládnout samo. A pokud dočtete až do konce, pak jste v těchto 5%!

Teď to nejdůležitější.

Pochopili jste teorii na toto téma. A opakuji, tohle... to je prostě super! Už teď jste lepší než drtivá většina vašich vrstevníků.

Problém je, že to nemusí stačit...

za co?

Za úspěšné složení jednotné státní zkoušky, za vstup na vysokou školu s omezeným rozpočtem a NEJDŮLEŽITĚJŠÍ, na celý život.

Nebudu tě o ničem přesvědčovat, řeknu jen jedno...

Lidé, kteří získali dobré vzdělání, vydělávají mnohem více než ti, kteří ho nezískali. Toto je statistika.

Ale to není to hlavní.

Hlavní je, že jsou VÍCE ŠŤASTNĚ (takové studie jsou). Možná proto, že se před nimi otevírá mnohem více příležitostí a život se stává jasnějším? nevím...

Ale zamyslete se sami...

Co je potřeba k tomu, abyste byli ve sjednocené státní zkoušce lepší než ostatní a nakonec byli... šťastnější?

ZÍSKEJTE SI RUKU ŘEŠENÍM PROBLÉMŮ NA TOMTO TÉMATU.

Při zkoušce se vás nebudou ptát na teorii.

budete potřebovat řešit problémy s časem.

A pokud jste je nevyřešili (HODNĚ!), určitě někde uděláte hloupou chybu nebo prostě nebudete mít čas.

Je to jako ve sportu – pro jistotu je potřeba to opakovat mnohokrát.

Najděte sbírku, kdekoli chcete, nutně s řešeními, podrobným rozborem a rozhodnout, rozhodnout, rozhodnout!

Můžete využít naše úkoly (volitelné) a my je samozřejmě doporučujeme.

Abyste mohli lépe používat naše úkoly, musíte pomoci prodloužit životnost učebnice YouClever, kterou právě čtete.

Jak? Jsou dvě možnosti:

1. Odemkněte všechny skryté úkoly v tomto článku -
2. Odemkněte přístup ke všem skrytým úkolům ve všech 99 článcích učebnice - Koupit učebnici - 899 RUR

Ano, takových článků máme v učebnici 99 a přístup ke všem úkolům a všem skrytým textům v nich lze okamžitě otevřít.

Přístup ke všem skrytým úkolům je poskytován po CELOU životnost webu.

A závěrem...

Pokud se vám naše úkoly nelíbí, najděte si jiné. Nezůstávejte jen u teorie.

„Rozumím“ a „Dokážu vyřešit“ jsou zcela odlišné dovednosti. Potřebujete obojí.

Najděte problémy a řešte je!

Pojem kolmých rovin

Když se dvě roviny protnou, dostaneme úhly vzepětí $4$. Dva úhly se rovnají $\varphi $ a další dva se rovnají $(180)^0-\varphi $.

Definice 1

Úhel mezi rovinami je minimem dihedrálních úhlů tvořených těmito rovinami.

Definice 2

Dvě protínající se roviny se nazývají kolmé, jestliže úhel mezi těmito rovinami je $90^\circ$ (obr. 1).

Obrázek 1. Kolmé roviny

Znak kolmosti dvou rovin

Věta 1

Pokud je přímka roviny kolmá k jiné rovině, pak jsou tyto roviny navzájem kolmé.

Důkaz.

Dostaneme roviny $\alpha $ a $\beta $, které se protínají podél přímky $AC$. Přímka $AB$ ležící v rovině $\alpha $ nechť je kolmá k rovině $\beta $ (obr. 2).

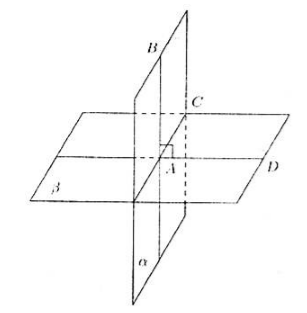
Obrázek 2

Protože přímka $AB$ je kolmá k rovině $\beta$, je také kolmá k přímce $AC$. Nakreslete navíc přímku $AD$ v rovině $\beta$, kolmou na přímku $AC$.

Zjistili jsme, že úhel $BAD$ je lineární úhel dihedrálního úhlu, rovný $90^\circ$. To znamená, že podle definice 1 je úhel mezi rovinami $90^\circ$, což znamená, že tyto roviny jsou kolmé.

Věta byla prokázána.

Z této věty vyplývá následující věta.

Věta 2

Pokud je rovina kolmá k přímce, podél které se protínají dvě další roviny, pak je také kolmá k těmto rovinám.

Důkaz.

Dostaneme dvě roviny $\alpha $ a $\beta $ protínající se podél přímky $c$. Rovina $\gamma $ je kolmá k přímce $c$ (obr. 3)

Obrázek 3

Protože přímka $c$ patří k rovině $\alpha $ a rovina $\gamma $ je kolmá k přímce $c$, pak podle věty 1 jsou roviny $\alpha $ a $\gamma $ kolmé.

Protože přímka $c$ patří k rovině $\beta $ a rovina $\gamma $ je kolmá k přímce $c$, pak podle věty 1 jsou roviny $\beta $ a $\gamma $ kolmé.

Věta byla prokázána.

Pro každý z těchto teorémů platí i obrácená tvrzení.

Ukázkové problémy

Příklad 1

Dostaneme pravoúhlý rovnoběžnostěn $ABCDA_1B_1C_1D_1$. Najděte všechny dvojice kolmých rovin (obr. 5).

Obrázek 4.

Řešení.

Podle definice pravoúhlého rovnoběžnostěnu a kolmých rovin vidíme následujících osm párů rovin navzájem kolmých: $(ABB_1)$ a $(ADD_1)$, $(ABB_1)$ a $(A_1B_1C_1)$, $( ABB_1)$ a $(BCC_1) $, $(ABB_1)$ a $(ABC)$, $(DCC_1)$ a $(ADD_1)$, $(DCC_1)$ a $(A_1B_1C_1)$, $(DCC_1) $ a $(BCC_1)$, $(DCC_1)$ a $(ABC)$.

Příklad 2

Dostaneme dvě vzájemně kolmé roviny. Z bodu v jedné rovině je nakreslena kolmice k jiné rovině. Dokažte, že tato přímka leží v dané rovině.

Důkaz.

Dostaneme kolmé roviny $\alpha $ a $\beta $ protínající se podél přímky $c$. Z bodu $A$ roviny $\beta $ je nakreslena kolmice $AC$ k rovině $\alpha $. Předpokládejme, že $AC$ neleží v rovině $\beta$ (obr. 6).

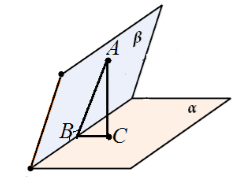
Obrázek 5.

Uvažujme trojúhelník $ABC$. Je obdélníkový s pravým úhlem $ACB$. Proto $\angle ABC\ne (90)^0$.

Ale na druhou stranu $\úhel ABC$ je lineární úhel dihedrálního úhlu tvořeného těmito rovinami. To znamená, že dihedrální úhel svíraný těmito rovinami není roven 90 stupňům. Zjistíme, že úhel mezi rovinami není roven $90^\circ$. Rozpor. Proto $AC$ leží v rovině $\beta$.

Tato lekce pomůže těm, kteří chtějí porozumět tématu „Znak kolmosti dvou rovin“. Na jeho začátku si zopakujeme definici dihedrálních a lineárních úhlů. Potom budeme uvažovat, které roviny se nazývají kolmé, a dokážeme znaménko kolmosti dvou rovin.

Téma: Kolmost přímek a rovin

Lekce: Znak kolmosti dvou rovin

Definice. Dihedrální úhel je obrazec tvořený dvěma polorovinami, které nepatří do stejné roviny, a jejich společnou přímkou ​​a (a je hrana).

Rýže. 1

Uvažujme dvě poloroviny α a β (obr. 1). Jejich společná hranice je l. Tento údaj se nazývá dihedrální úhel. Dvě protínající se roviny svírají čtyři dihedrální úhly se společnou hranou.

Dihedrální úhel se měří jeho lineárním úhlem. Zvolíme libovolný bod na společné hraně l úhlu dihedrálního úhlu. V polorovinách α a β vedeme z tohoto bodu kolmice a a b k přímce l a získáme lineární úhel úhlu vzepětí.

Přímky a a b svírají čtyři úhly rovné φ, 180° - φ, φ, 180° - φ. Připomeňme, že úhel mezi přímkami je nejmenší z těchto úhlů.

Definice. Úhel mezi rovinami je nejmenší z dihedrálních úhlů tvořených těmito rovinami. φ je úhel mezi rovinami α a β, jestliže

Definice. Dvě protínající se roviny se nazývají kolmé (vzájemně kolmé), pokud je mezi nimi úhel 90°.

Rýže. 2

Na hraně l je vybrán libovolný bod M (obr. 2). Nakreslete dvě kolmé přímky MA = a a MB = b k hraně l v rovině α a v rovině β. Máme úhel AMB. Úhel AMB je lineární úhel dihedrálního úhlu. Je-li úhel AMB 90°, pak se roviny α a β nazývají kolmé.

Čára b je konstrukčně kolmá na čáru l. Přímka b je kolmá k přímce a, protože úhel mezi rovinami α a β je 90°. Zjistíme, že přímka b je kolmá ke dvěma protínajícím se přímkám a a l z roviny α. To znamená, že přímka b je kolmá k rovině α.

Podobně můžeme dokázat, že přímka a je kolmá k rovině β. Přímka a je konstrukčně kolmá na přímku l. Přímka a je kolmá k přímce b, protože úhel mezi rovinami α a β je 90°. Zjistíme, že přímka a je kolmá na dvě protínající se přímky b a l z roviny β. To znamená, že přímka a je kolmá k rovině β.

Pokud jedna ze dvou rovin prochází přímkou ​​kolmou k druhé rovině, pak jsou takové roviny kolmé.

Dokázat:

Rýže. 3

Důkaz:

Nechť se roviny α a β protínají podél přímky AC (obr. 3). Abyste dokázali, že roviny jsou vzájemně kolmé, musíte mezi nimi sestrojit lineární úhel a ukázat, že tento úhel je 90°.

Přímka AB je kolmá k rovině β, a tedy k přímce AC ležící v rovině β.

Narýsujme přímku AD kolmou k přímce AC v rovině β. Potom BAD je lineární úhel dihedrálního úhlu.

Přímka AB je kolmá k rovině β, a tedy k přímce AD ​​ležící v rovině β. To znamená, že lineární úhel BAD je 90°. To znamená, že roviny α a β jsou kolmé, což bylo potřeba dokázat.

Rovina kolmá k přímce, podél které se protínají dvě dané roviny, je kolmá na každou z těchto rovin (obr. 4).

Dokázat:

Rýže. 4

Důkaz:

Přímka l je kolmá k rovině γ a rovina α prochází přímkou ​​l. To znamená, že na základě kolmosti rovin jsou roviny α a γ kolmé.

Přímka l je kolmá k rovině γ a rovina β prochází přímkou ​​l. To znamená, že podle kolmosti rovin jsou roviny β a γ kolmé.